Chapter 11 線形モデル(回帰分析)
これまで学んできた様々な統計手法(t検定、分散分析など)を、「線形モデル」という一つの枠組みで捉えていく。
この章では「線形モデル」の一部である回帰分析を通して、線形モデルの概要を学んでいく。
11.2 線形モデルの概要
まず、線形モデルの表現の仕方を理解する。以下の式は、変数\(x\)から、変数\(y\)を予測するプロセスを記述したものである。変数\(x\)は予測変数(predictor variable)、変数\(y\)は応答変数(response variable)と呼ばれる。このように、応答変数と予測変数との関係を式で表現したものをモデルと呼ぶ。
予測変数は、「独立変数」や「説明変数」とも呼ばれる。応答変数は、「従属変数」や「被説明変数」とも呼ばれる。
\[ \begin{equation} \mu = \alpha + \beta x \tag{1}\\ y \sim \text{Normal}(\mu, \sigma) \end{equation} \]
1番目の式の右側に\(\alpha + \beta x\)という線形の式がある。この式は、線形予測子(linear predictor)と呼ばれる。変数\(x\)に係る\(\beta\)は予測変数に係る傾き(slope)、\(\alpha\)は切片(intercept)である。1番目の式は、変数\(x\)の持つ効果(傾き)及びそれ以外の効果(切片)と変数\(y\)の予測値(\(\mu\))との関係を示している。
予測変数は2個以上でも構わない。予測変数の個数を\(K\)とすると、(1)の1番目の式は以下のように表現できる。
\[ \begin{equation} \mu = \alpha + \sum_{k=1}^{K} \beta_{k} x_{k} \\ \tag{2} \end{equation} \]
\(y \sim \text{Normal}(\mu, \sigma)\)は、「応答変数\(y\)が、\(\mu\)を平均、\(\sigma\)を標準偏差とする正規分布に従う」ことを示している。つまり、線形予測子から予測された値\(\mu\)と誤差\(\sigma\)から、実際の値\(y\)が推定されるプロセスを表現している。
応答変数が正規分布に従うという前提をおいたモデルのことを、一般的に線形モデル(linear model)と呼ぶ。
線形モデルは、基本的に心理統計でも学んだ「回帰分析(regression analysis)」と同じである。
応答変数\(y\)を決定づける変数、\(\alpha\), \(\beta\)、及び \(\sigma\)はパラメータ(parameter)と呼ばれる。このパラメータを、既知の変数である\(x\)と\(y\)から推定する。
11.3 線形モデルによる解析
実際に、Rで線形モデルの解析をしてみよう。
Rには線形モデルを扱える関数lm()がある。irisデータを使って解析をしてみよう。
Sepal.LengthとPetal.Lengthの関係を散布図で確認する。
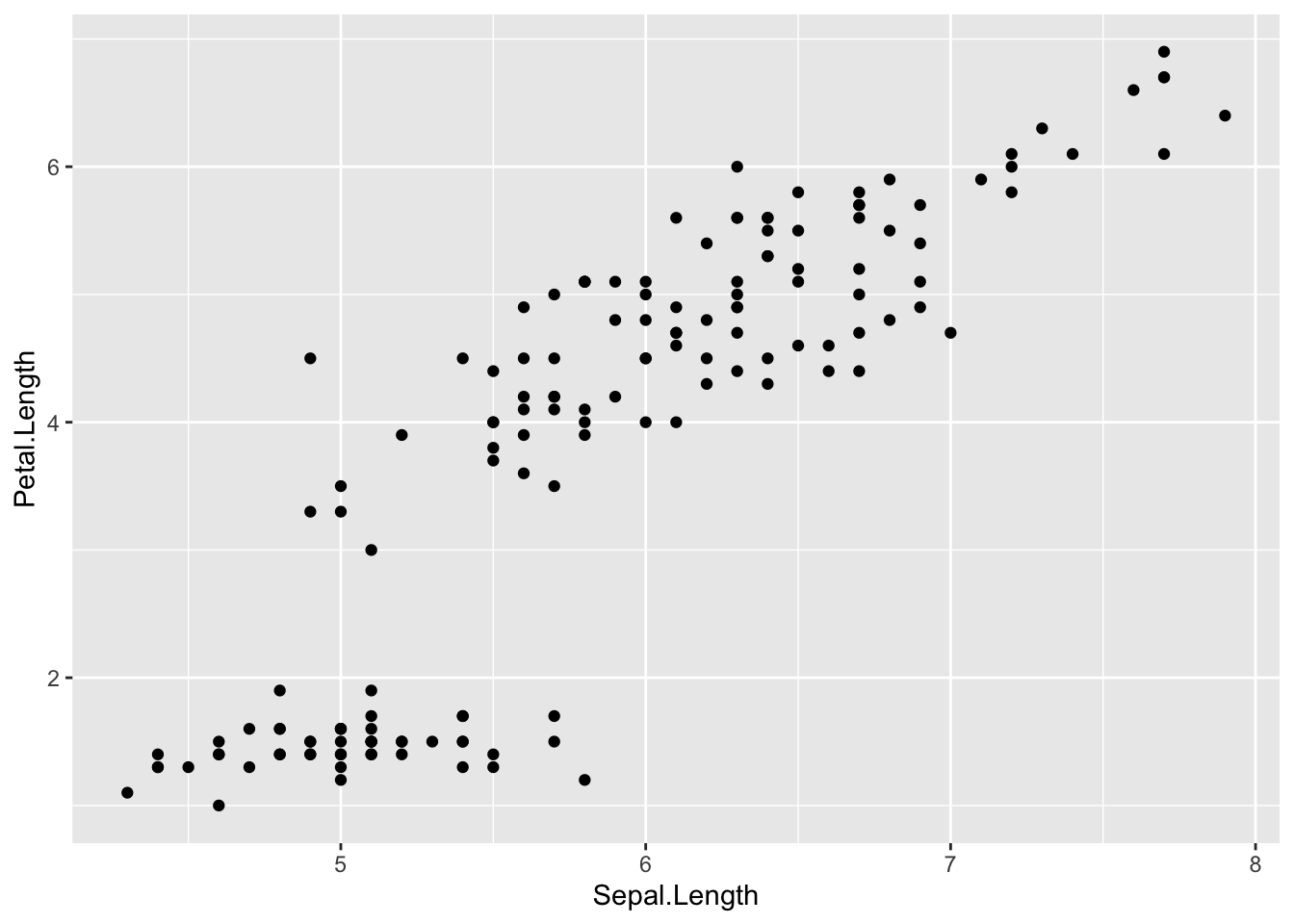
Sepal.Lengthが大きいほどPetal.Lengthが大きいという関係(正の相関)がありそうである。そこで、Sepal.Lengthの大きさから、Petal.Lengthの大きさを予測することを試みる。
lm()関数に、「応答変数~ 1 + 予測変数」のかたちで入力する。以下のプログラムを実行してみよう。
*1 +の部分は省略しても構わない。1 +は線形予測子の切片の部分を表している。省略しても、lm()は自動で切片の値を求めてくれる。
結果をresultという名前でいったん保存した(名前はresult以外でも構わない)。summary()関数の中に、resultを入れて実行すると詳細な結果が出力される。
##
## Call:
## lm(formula = Petal.Length ~ 1 + Sepal.Length, data = iris)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.47747 -0.59072 -0.00668 0.60484 2.49512
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.10144 0.50666 -14.02 <2e-16 ***
## Sepal.Length 1.85843 0.08586 21.65 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8678 on 148 degrees of freedom
## Multiple R-squared: 0.76, Adjusted R-squared: 0.7583
## F-statistic: 468.6 on 1 and 148 DF, p-value: < 2.2e-16色んな情報が出力されるが、まずは係数(Coefficients)の部分を見てみよう。ここでは、データから推定された切片や予測変数の傾きの結果が出力されている。
- Interceptの部分が切片の推定結果である。各変数の名前の部分(ここではSepal.Length)が予測変数の傾きの推定結果を示している。
- Estimateが推定された切片または傾きの値である。
- Std.Errorは推定された係数の標準誤差である。
予測変数が応答変数に対して影響力を持っているか? それは傾きの係数の推定結果からわかる。係数の値は、予測変数が1単位増えたら応答変数がどのくらい増えるか、あるいは減るかを意味している。
係数がプラスならば、予測変数の値が増えると応答変数の値が増加する関係にあることを意味する。
係数がマイナスならば、予測変数の値が増えると応答変数が減少する関係にあることを意味する。
t value及びPrは係数の有意性検定の結果を示している(それぞれt値、p値)。ここでは、「母集団の係数がゼロである」という帰無仮説を検定している。p値が極端に低い場合は、「求めた係数の値は有意にゼロから離れている」と結論付けることができる。
この例の場合は、Sepal.Lengthが1単位増えると、Petal.Lengthが1.86だけ上昇することを示している。
切片の値は-7.1となっているが、Sepal.Lengthの値がゼロのときのPetal.Lengthの予測値を意味している(この例ではアヤメのがくの長さとしてありえない負の値になっているが、これは変数の標準化等を行っていないためである。詳しくは次章で解説する)。
Sepal.LengthとPetal.Lengthの散布図に、線形モデルから推定された切片と傾きの値を持つ以下の直線を引いてみよう。
\[ \begin{equation} Petal.Length = -7.10 + 1.86 Sepal.Length\\ \tag{3} \end{equation} \]
p = ggplot2::ggplot() +
ggplot2::geom_point(data = iris, aes(x = Sepal.Length, y = Petal.Length)) +
ggplot2::geom_smooth(data = iris, aes(x = Sepal.Length, y = Petal.Length), formula = y~x, method = "lm", se = FALSE)
p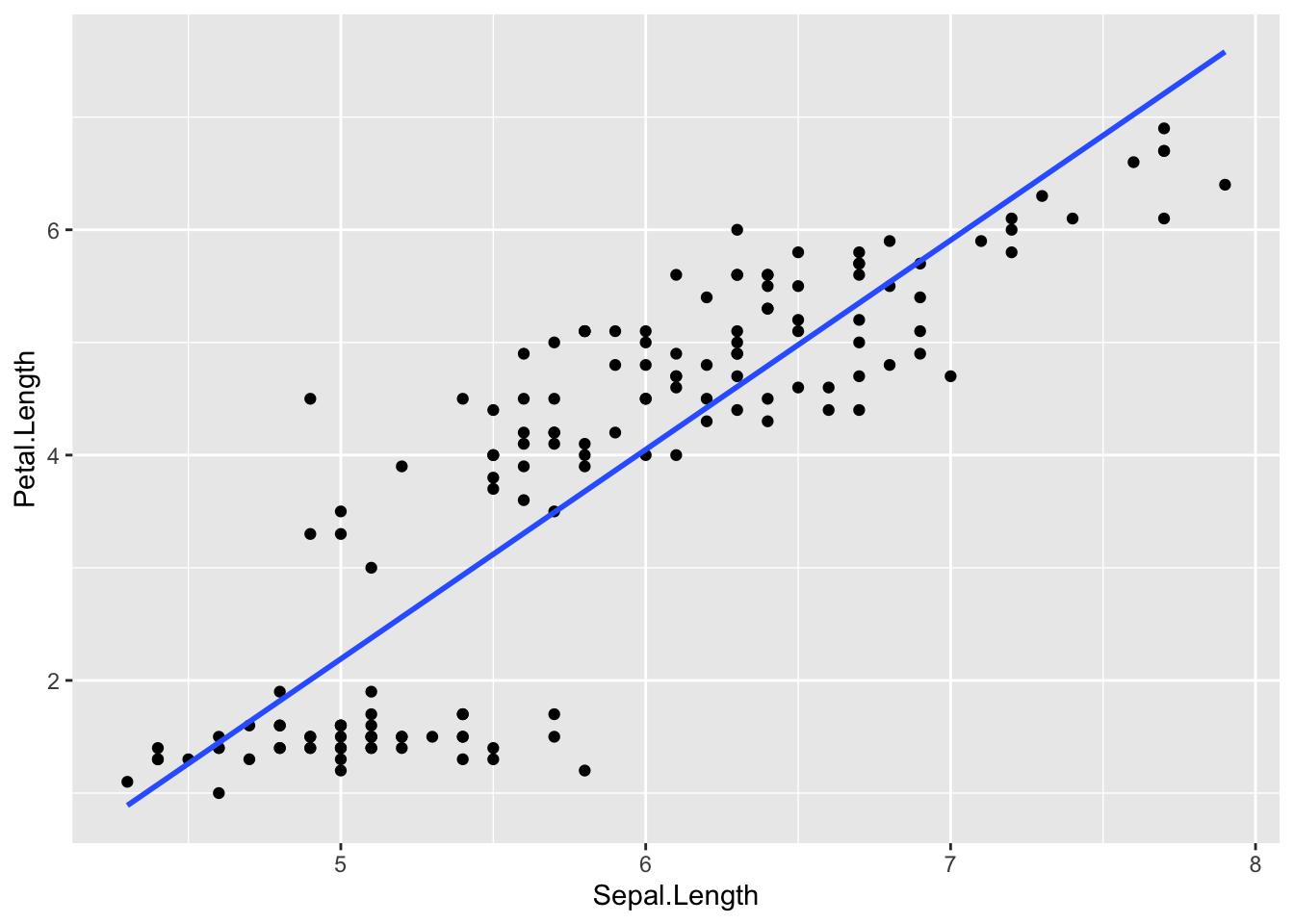
線形モデルでは、直線の式で予測変数と応答変数の関係を表現する。実際のデータ(散布図の点)とのズレが最小になるような、直線の式を推定する(予測値と実測値とのズレが最小になるのが、最も良い予測である)。
11.4 最尤法
(ここでは、線形モデルのパラメータがどのように推定されているかについて解説している。読み飛ばしても、線形モデルを使った解析自体はできる)
線形モデル(及び一般化線形モデル)では、パラメータの推定に最尤法(maximum likelihood method)という最適化手法が用いられる。
11.4.1 最尤法によるパラメータ推定
ここにコインが1枚ある。コインの表が出るかを決定づけるパラメータ(つまりコインを投げて表が出る確率)を\(\theta\)(シータ)とする。この\(\theta\)の値を何回かコインを投げる実験を通して推定する。
1回目は、表が出た。この時点で、この実験結果が生じる確率は\(\theta\)である。
2回目は、裏が出た。1回目と2回目までの実験結果が生じる確率は\(\theta(1-\theta)\)である。
3回目は、表が出た。ここまでの実験結果が生じる確率は\(\theta(1-\theta)\theta\)である。
その後、4回目は裏、5回目は裏だったとする。5回目で実験をストップすることにする。この実験結果が生じる確率\(L\)は以下のように表すことができる。
\[ L = (1-\theta)^3 \theta^2 \tag{4} \]
\(L\)のことを尤度(likelihood)と呼ぶ(”ゆうど”と読む)。
尤度とは「もっともらしさ」を示す概念である。イメージとしては、「今回の観測結果が得られる確率」である。今回の観測データに対して最も当てはまりが良くなる、すなわち尤度が最も高くなるときのパラメータを求めるのが、最尤法 と呼ばれる手法である。
掛け算を扱う尤度は計算が困難なので、実際のパラメータ推定の際には対数化して足し算を扱う。対数化した尤度を対数尤度(log-likelihood)と呼ぶ。対数尤度が最大となるパラメータ\(\theta\)を求める。
\[ \log L = \log(1-\theta)+\log(1-\theta)+\log(1-\theta)+\log(\theta)+\log(\theta) \tag{5} \]
以下のプログラムで、上のコイン投げの例で最も対数尤度が高くなるときの\(\theta\)を求めている。maximumが対数尤度が最も高くなるパラメータの値で、objectiveがそのときの対数尤度である。(プログラムの意味については理解しなくて良い)
D = c(1, 0, 1, 0, 0) #観測データのベクトル:1=表、0=裏とする
#対数尤度を求める関数
LogLikelihood = function(par) {
theta = par
#確率の制約(0 < theta_2 < 1)
theta_2 = min(max(theta, 1e-10), 1 - 1e-10)
ll <- sum(D * log(theta_2) + (1 - D) * log(1 - theta_2))
return(ll)
}
#対数尤度が最も大きいときのパラメータ(theta)を推定する
#optimは最小化の最適化関数なので、対数尤度を負にして最適化する
int = 0 # パラメータの初期値
result_mlm = optim(par = int,
fn = function(p) - LogLikelihood(p),
method = "L-BFGS-B",
hessian = TRUE)
result_mlm$par #推定されたパラメータ## [1] 0.4000003推定された「表が出る確率」は、実験で表が出た回数の割合と一致している。
## [1] 0.4パラメータ\(\theta\)と対数尤度\(\log L\)との関係を以下に示す。
#図示する
theta = seq(0.01,0.99,0.01)
logL = log(theta)+log(1-theta)+log(theta)+log(1-theta) + log(1-theta)
data_mlm = data.frame(x=theta, y=logL)
ggplot2::ggplot() +
ggplot2::geom_line(data = data_mlm, aes(x = x, y = y), linewidth = 1) +
ggplot2::geom_vline(xintercept = result_mlm$par, linetype = "dashed", colour = "red", size = 1) +
ggplot2::labs(x ="theta", y = "log L") 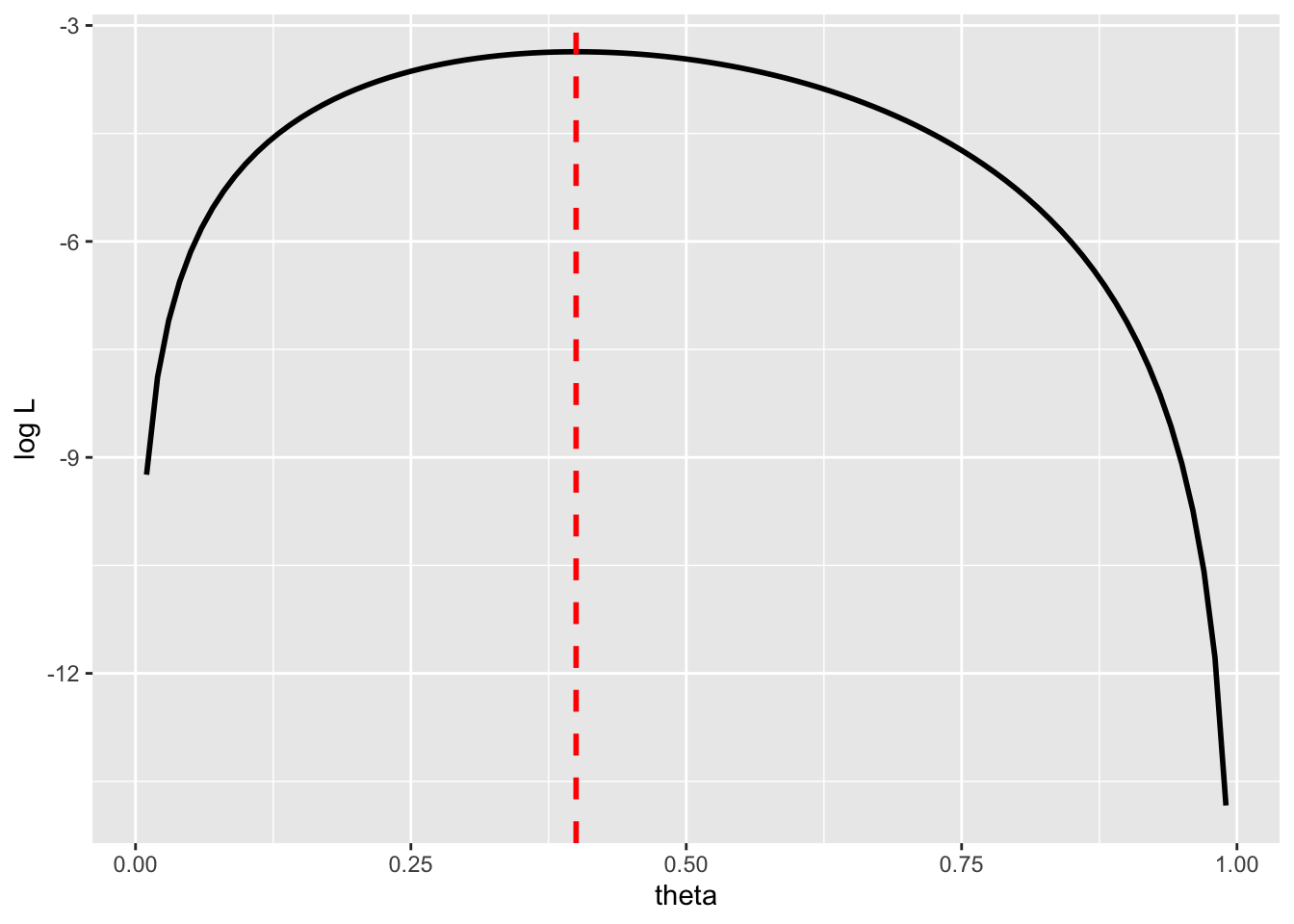
対数尤度が最も大きくなるのは、\(\theta=\) 0.4のときである。
11.4.2 最尤法による線形モデルのパラメータ推定
先ほどの例ではわかりやすいように、パラメータを1つのみ使って説明をした。線形モデルの傾きや切片を推定する場合も同様である。上の例の\(\theta\)を、線形予測子に置き換えて同様の計算をする。
まずは、xとyの2つの変数からなるデータを作成し、xを予測変数、yを応答変数とした線形モデルを行う。傾き及び切片も任意のものに指定する。
#データの作成
n = 100 #データ数
x = runif(n, 0, 1) #予測変数(一様分布から乱数を生成)
#線形モデルのパラメータを指定する
alpha = 2.5 #切片
beta = 0.8 #傾き
sigma = 1 #正規分布の標準偏差
mu = alpha + beta * x
y = rnorm(n, mu, sigma) #応答変数
d = data.frame(x = x, y = y)
head(d)## x y
## 1 0.2655087 3.110513
## 2 0.3721239 2.185673
## 3 0.5728534 3.299402
## 4 0.9082078 2.097203
## 5 0.2016819 4.094369
## 6 0.8983897 5.199112対数尤度を求め、対数尤度が最大となるパラメータを推定する。
#対数尤度関数の定義
log_likelihood = function(params) {
alpha = params[1]
beta = params[2]
sigma = params[3]
mu = alpha + beta * d$x
ll = sum(dnorm(d$y, mean = mu, sd = sigma, log = TRUE)) #確率密度の対数の和
return(ll)
}
#対数尤度が最も大きいときのパラメータ(par)を推定する
#optimは最小化の最適化関数なので、対数尤度を負にして最適化する
int = c(alpha = 0, beta = 1, sigma = 2) #パラメータの初期値の指定
result_mle = optim(par = int,
fn = function(p) - log_likelihood(p),
method = "L-BFGS-B",
lower = c(-Inf, -Inf, 1e-10))
result_mle$par## alpha beta sigma
## 2.3206740 1.1123416 0.9316027lm()で推定されたパラメータと一致することを確認する。
##
## Call:
## lm(formula = y ~ x, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.84978 -0.56222 -0.08707 0.52427 2.51661
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.3207 0.2058 11.276 < 2e-16 ***
## x 1.1123 0.3535 3.147 0.00219 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9411 on 98 degrees of freedom
## Multiple R-squared: 0.09178, Adjusted R-squared: 0.08252
## F-statistic: 9.904 on 1 and 98 DF, p-value: 0.002185線形モデルのパラメータ推定には、最小二乗法という方法もある。最小二乗法は、応答変数の実測値と予測値の差の絶対値の合計(残差)が最小になるときの切片及び傾きを求める方法である。ただし、最小二乗法でも最尤法でも、線形モデルの傾きや切片の推定値は同じになる。
例えば、以下の線形モデルの切片及び傾きのパラメータを推定するとする。
\[ \mu = \alpha + \beta x\\ y \sim \text{Normal}(\mu, \sigma) \] データを\(y_{1}, y_{2}, ..., y_{n}\)とすると、正規分布の確率密度関数より、
\[ f(y_{i}) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(y_i-\mu_{i})^2}{2\sigma^2}\right) \]
尤度関数Lは、
\[ L = \prod_{i=1}^{n} f(y_{i}) \\ = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(y_{i}-\mu_{i})^2}{2\sigma^2}\right) \]
となる。第7章でも解説しているように連続量の場合は個々のデータの確率を求めることはできないので、尤度は確率密度をかけ合わせたものを用いる。
対数尤度は
\[ \log L = \sum_{i=1}^{n}-\frac{1}{2} \log(2\pi\sigma^2) - \sum_{i=1}^{n}\frac{{(y_{i}-\mu_{i})^2}}{2 \sigma^2}\\ = -\frac{n}{2} \log(2\pi\sigma^2) - \frac{1}{2 \sigma ^2}\sum_{i=1}^{n} (y_{i}-\mu_{i})^2 \]
となる。\(\mu_{i} = \alpha + \beta x_{i}\)を代入すると
\[ \log L = -\frac{n}{2} \log(2\pi\sigma^2) - \frac{1}{2 \sigma ^2}\sum_{i=1}^{n} (y_{i}-(\alpha + \beta x_{i}))^2 \] となる。\(\alpha\)と\(\beta\)の値によって決まるのは2つ目の項である。 つまり、対数尤度\(\log L\)を最大にする\(\alpha\)と\(\beta\)を求めることは、\(\sum_{i=1}^{n}(y_{i} - (\alpha + \beta x_{i}))^2\)を最小化する\(\alpha\)と\(\beta\)を推定することと同じである。そのため、最小二乗法と最尤法で推定される結果は同じになる。